In mathematics, relations and functions form one of the most important concepts that connect various topics like algebra, trigonometry, and calculus. A relation is a connection between two sets. In this article we deeply study types of relations, types of functions, composition of functions, and invertible functions.
What are relations?
A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product \(A\times B\).
Thus, R is a relation from A to B \(\iff R\subseteq A\times B\).
\( \iff R \subseteq {(a,b): a\in A, b\in B }\). It is also written as aRb.
Example: Let A={1, 2, 3} and B={4, 5} and let R={(1,4), (1,5), (2,4),(2,5), (3,4), (3,5)}. Here, \(R \subseteq A\times B \) so, R is a relation from A to B.
But, if R={(1,2), (3,4), (4,6)}. Here,\( R\not\subset A\times B\). so, R is not relation from A to B. Since, \((4,6)\in R\) but \((4,6)\not\in A\times B\)
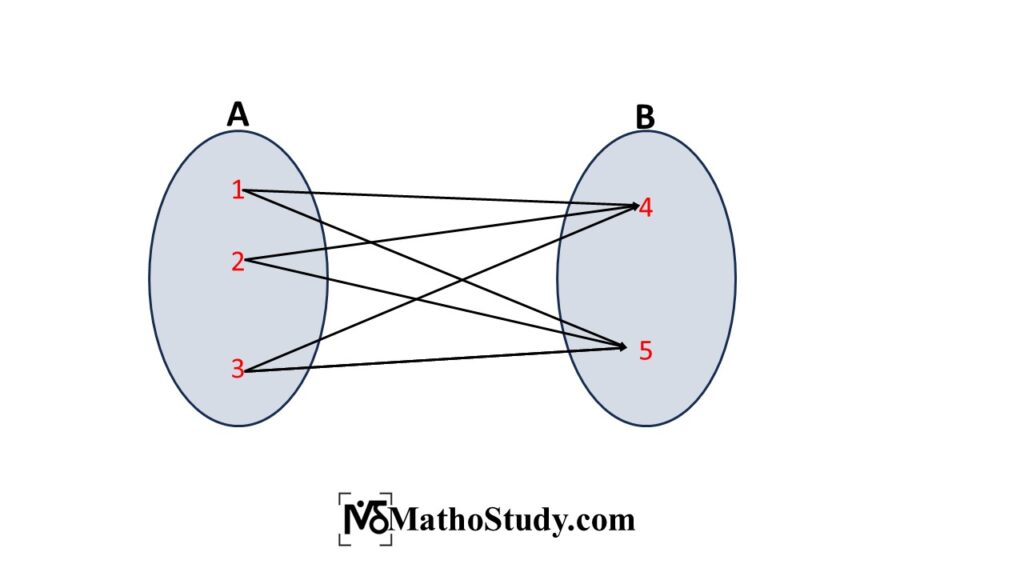
Types of relations
(a) Empty or void relations: A relation R is called an empty or void relation if no element of A is related to any element of B, i.e. \(R=\phi \subset A\times B \). Example: Let A={2,3,4} and B={7,11} let \(R={(a,b):a\in A,b\in B \:and\: b\div a \:is \:integer}\)
Here, R is an empty relation.
(b) Universal relation: A relation R is called universal relation if each elements of A related to every element of B. i.e., \(R=A\times B \).
Example: Let A={1,2} and B= {3,4}.
Let R={(1,3), (1,4), (2,3),(2,4)}.
Here \(R=A\times B\).
So, Relation R is a universal relation.
(c). Identity relation: A relation R is called an identity relation on A if each element of A is related to the same element of A, i.e., \(R=I_{A}=\{(a,a): \forall \:a\in A \}\). Example: Let A={1,2,3} Let IA ={(1,1),(2,2),(3,3)}.
(d). Reflexive relation: A relation R defined on a set A is said to be reflexive. if aRb for all \(a\in A \), i.e., \((a,b)\in R, \forall \: a\in A \).
Example: Let A={1,2,3),
Then R={(1,1),(2,2),(3,3)} is a reflexive relation on A.
(e). Symmetric relation: A relation R defined on a set A is said to be symmetric. if \[(a,b)\in R \Rightarrow (b,a)\in R, \forall \: a,b \in A \] i.e., \(aRb \Rightarrow bRa \). Example: Let A={1,2,3),
Then R={(1,2),(2,1),(2,3), (3,2)} is a symmetric relation on A.
(f). Transitive relation: A relation R defined on a set A is said to be transitive. if \[(a,b)\in R\: and \: (b,c)\in R \Rightarrow (a,c)\in R, \forall \: a,b,c \in A \] i.e., \(aRb \: and \: bRc \Rightarrow aRc \). Example: Let A={1,2,3}.
Then R={(1,2),(2,3),(1,3)} is a transitive relation on A.
What is an equivalence relation?
Let A be a non-empty set, then a relation R on A is said to be equivalence relation if
- R is reflexive: \((a,b)\in R, \forall \: a\in A \).
- R is symmetric: \[(a,b)\in R \Rightarrow (b,a)\in R, \forall \: a,b \in A \] i.e., \(aRb \Rightarrow bRa \).
- R is transitive: \[(a,b)\in R\: and \: (b,c)\in R \Rightarrow (a,c)\in R, \forall \: a,b,c \in A \] i.e., \(aRb \: and \: bRc \Rightarrow aRc \).
Here, R is reflexive, symmetric, and transitive. So, R is an equivalence relation on A.
What is a function?
Let A and B be two non-empty sets. Then a rule f, which associates each element of A with a unique element of B, is called a function. Example: Let A={1,2} and B={a,b} then f={(1,a), (2,b)} is a function.
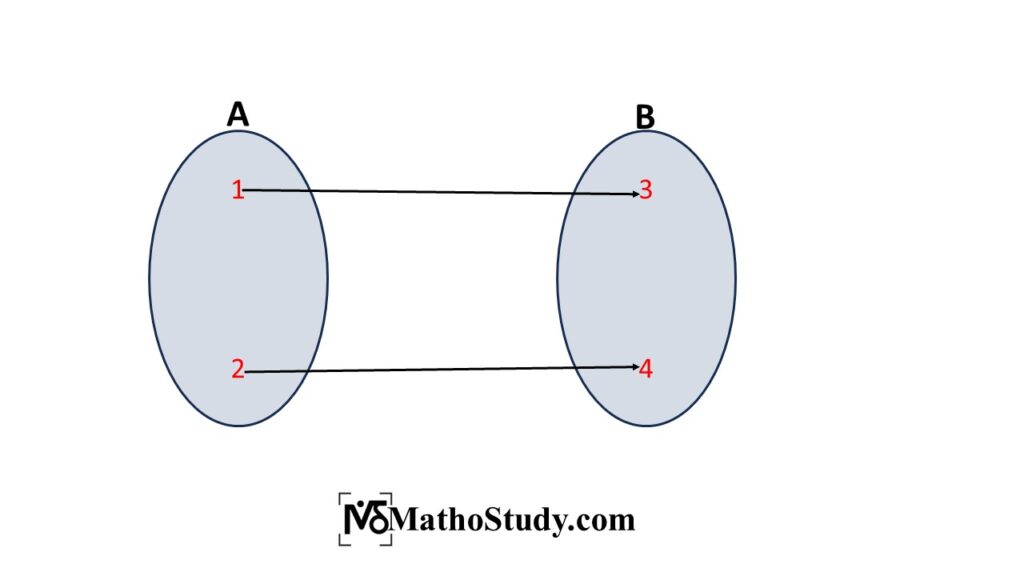
Types of Functions
(i) One-one function (Injective function or Injection): A function f : A → B is one-one function or injective function if distinct elements of A have distinct images in B.Thus, f : A → B is one-one ⇔ \(f(a)=f(b) ⇒ a= b, ∀ \: a, b\in A \)
⇔ \(a\not= b \Rightarrow f(a)\not =f(b), \forall \: a,b\in A \)
Note: (a) If A and B are two sets having m and n elements respectively such that m ≤ n, then total number of one-one functions from set A to set B is nCm × m ! i.e., nPm.
(b) If n(A) = m, then the number if injective functions defined from A onto itself is m!.
Algorithm to check the Injectivity of a Function :
Step 1: Take any two arbitrary elements a, b in the domain of f.
Step 2: Put f (a) = f (b)
Step 3: Solve f (a) = f(b). If it gives a = b only, then f is one-one function
(ii) Many-one function: If any two or more elements of set A are related to a single element of set B, then we call this function as many-one function.
Thus, f : A → B is many-one ⇔ \(f (a) = f (b) ⇒ a ≠ b, ∀\: a, b ∈ A\)
(iii) Onto function (Surjective function or Surjection): A function f : A → B is onto function or a surjective function if every element of B is image of some element of A. That implies f(A) = B or range of f is the co-domain of f.
Thus, f : A → B is onto ⇔ f (A) = B i.e., range of f = co-domain of f
Algorithm to check the Surjectivity of a Function :
Step 1: Take an element \(b\in B\), where B is the co-domain of the function.
Step 2: Put f (x) = b.
Step 3: Solve the equation f(x) = b for x and obtain x in terms of b. Let x = g(b).
Step 4: If for all values of \(b\in B\), the values of x obtained from x = g(b) are in A, then f is onto. If there are some \(b\in B\) for which values of x, given by x = g(b), are not in A. Then, f is not onto.
(iv) Into function: Function ‘f’ from set A to set B is an into function if set B has atleast an element which is not related to any of the elements of set A.
(v) One-one onto function (Bijective function or Bijection): A function f : A → B is said to be one-one onto or bijective if it is both one-one and onto i.e., if the distinct elements of A have distinct images in B and each element of B is the image of some elements of A. Also, note that a bijective function is also called a one-to-one function or one-to-one correspondence.
Difference between relations and functions :
| S. No. | Relation | Function |
|---|---|---|
| 1 | There may be some elements of A which are not related to any element of B. | Each elements of A is related to some element of B. |
| 2 | An element of A may be related to more than one element of B. | An element of A is not be related to more than one element of B. |
Some Important Questions On Relations and Functions
Q1. Let A = {1, 2, 3} and B = {4, 5}. Find the number of all possible relations from A to B.
Solution: A relation from A to B is a subset of \(A \times B \). \[A \times B = \{(1,4), (1,5), (2,4), (2,5), (3,4), (3,5)\}\]. Number of elements in \(A \times B = 6\)
Therefore, number of relations from A to B \(= 2^{6} = 64\)
Q2.Let R be a relation on the set Z defined by R = \(\{(a, b): a – b \in Z\}\). Is R an
equivalence relation?
Solution: We check the three properties:
Reflexive: \(a – a = 0 \in Z \Rightarrow (a, a) \in R\).
Symmetric: If \((a, b) \in R \Rightarrow a – b \in Z \Rightarrow -(a – b) = b – a \in Z \Rightarrow (b, a) \in R\).
Transitive: If \((a, b) \in R\) and \((b, c) \in R\), then \(a – b \in Z\) and \(b – c \in Z \Rightarrow (a – b) + (b – c) = a – c \in Z\Rightarrow (a, c) \in R\).
Hence, R is an equivalence relation
Q3.Check whether the function \(f: R \to R \) defined by \(f(x)
= x^{2}\) is one-one and onto.
Solution:One-one:
Suppose \(f(x_{1}) = f(x_{2})\).
Then \(x_{1}^{2} = x_2^2 \Rightarrow x_1 = x_2 \:or \:x_1 = -x_2 \).
Hence, f is not one-one.
Onto: For \(y \in R \), check if there exists x such that \(f(x) = y\) But \(x^2 \geq 0 \Rightarrow f(x)\) cannot take negative values
Hence, f is not onto.
So, f is neither one-one nor onto.
FAQs on Relations and Functions
Q1. What is the difference between a relation and a function?
Answer: A relation from set A to set B is a subset of the Cartesian product \(A \times B\). A function is a special type of relation where every element of A is
related to exactly one element in B.
Q2. How many relations are possible from set A to set B?
Answer: If n(A)=p and n(B)=q, then total number of relations \(=2^p\times q\)
Q3. How many functions are there from A to B?
Answer: If n(A)=p and n(B)=q, then total number of functions\(=q^p\).
Q4. What is a bijective function?
Answer: A function is bijective if it is both one-one and onto.




