Number Systems

The number systems represent the foundation of mathematics. It refers to a set of all numbers used in calculations and their classification into different types. In Class 9, learning the number system is important because it provides the foundation for algebra, geometry, and higher mathematics.

Types of Numbers in the Number Systems

(1). Natural Numbers – Numbers which comes naturally to us. Natural numbers denoted by N. count the number of fingers in our hand 1,2,3……, these are natural number.
Example: N= {1,2,3, 4, …….}

(2). Whole numbers- All natural numbers including ‘0’ is called whole numbers. Whole numbers denoted by W.
Example: W= {0, 1, 2, 3, 4, ……}

(3). Integers- All whole numbers including negative numbers (…., -3, -2,-1) is called integers. Integers denoted by I or Z.
Example: Z= {……, -3, -2, -1, 0,1, 2, 3, ……}
Note-Z comes from German word “Zahlen” which means “to count”

(4). Rational numbers-A numbers which can be written in the form p/q is called rational numbers where p and q are integers and q≠0. Rational numbers denoted by Q and Q comes from the word ‘quotient’

(5). Irrational numbers– A numbers which can not be written in the form p/q is called irrational number swhere p and q are integers and q≠0.

(6). Real numbers- All the numbers which containing rational and irrational numbers is called real numbers (The numbers represented on a number line are called real numbers ). It is denoted by R.

Property of rational numbers:

The decimal expansion of a rational number is either terminating or non-terminating repeating. Thus we say that a number whose decimal expansion is either terminating or non-terminating repeating is a rational number.

Property of irrational number:

The decimal expansion of an irrational number is non-terminating and non-repeating. Moreover, a number whose decimal expansion is non-terminating and non-repeating is irrational.

Terminating decimal- It has a finite number of digits after the decimal point. e.g. 8/16=0.5625

Non-terminating decimal-It has a digit or group of digits after the decimal point that repeat endlessly. e.g. √2,√3,√5.

Representation of Irrational Numbers on the Number Line

Let √a be an irrational number. To represent it on the number line we will follow the following steps-
Take any point A. Draw a line AB = a units. Extend AB to point C such that BC = 1 unit. Find out the mid-point of AC and name it ‘O’. With ‘O’ as the centre draw a semi-circle with radius OC. Draw a straight line from B which is perpendicular to AC, such that it intersects the semi-circle at point D. Length of BD=√a.

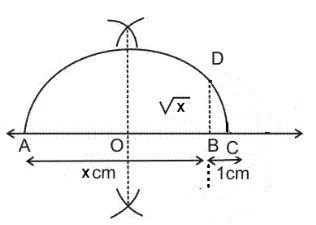
Constructions to Find the root of a. With BD as the radius and B as the centre, cut the positive side of the number line to get √a.

Operations on Real Numbers:

 Let a and b be real numbers. Then

(i)√(ab) = √a√b
(ii)(√a+√b) (√a-√b) = a – b
(iii)(a+√b)(a−√b) = a²−b
(iv)(√a+√b)(√c+√d) = √ac+√ad+√bc+√bd
(v)(√a+√b)(√c−√d) = √ac−√ad+√bc−√bd
(vi)(√a+√b)² = a+2√(ab)+b

Rationalisation: Rationalisation is the process of converting an irrational number into a rational number.
e.g. rationalisation of 1/(√a+√b)
1/(√a+√b)=1/(√a+√b) × (√a-√b)/(√a-√b)=(√a-√b)/(a-b)

Laws of exponents for real numbers: Let a > 0 and b > 0 be a real number and p and q be rational numbers. Then, we have
(i) a^p.a^q=a^p+q

(ii)(a^p)^q=a^pq

(iii)a^p/a^q=a^p-q

(iv)a^p.b^p=(ab)^p

Important Questions on Number Systems

Question 1. Is \(\frac{22}{7} \) is a rational number ?

Answer: Yes, because it can be written as \(\frac{p}{q} \), where p,q are integer.

Question 2. Is \(\sqrt{2} \) rational or irrational number?

Answer: Irrational number because it can not expressed in form \(\frac{p}{q} \)

Frequently Asked Questions (FAQs) on Number Systems

Q1: Is 0 a natural number?
Answer: No, 0 is a whole number but not a natural number.

Q2: Are all rational numbers real?
Answer: Yes, all rational numbers are part of the real number system.

Q3: Is \(\pi \) rational?
Answer: No, \(\pi \) is irrational.