Lines and Angles form the foundation of geometry and are vital for understanding shapes, proofs, and construction problems in higher mathematics. In Class 9 Chapter 6 of NCERT Maths, we explore various types of angles, relationships between lines, and important theorems to build a strong conceptual base.
Point: A point is a position represented by a fine dot(.) on paper by a sharpened pencil or pen. A point does not have any length, width, shape, or size.
Line: A line is a straight path formed by connecting a set of points on a plane. It has length but no width and height. A line extends indefinitely in both the directions. Line AB is represented as AB.
Line segment: A part (or portion) of a line with two end points is called a line segment.

Ray: A part of a line with one end point is called a ray.

Collinear points: If three or more points lie on the same line, they are called collinear points; otherwise, they are called non-collinear points.
Types of Angles:
- Acute angle: An acute angle measure between 0° and 90°.
- Right angle: A right angle is exactly equal to 90°.
- Obtuse angle: An angle greater than 90° but less than 180°
- Straight angle: A straight angle is equal to 180°.
- Reflex angle: An angle which is greater than 180° but less than 360° is called a reflex angle.
- Complete angle: A complete angle is equal to 360°.
| Angle Type | Measure Range |
|---|---|
| Acute Angle | 0° < angle < 90° |
| Right Angle | Exactly 90° |
| Obtuse Angle | 90° < angle < 180° |
| Straight Angle | Exactly 180° |
| Reflex Angle | 180° < angle < 360° |
| Complete Angle | Exactly 360° |
Complementary angles: Two angles whose sum is 90° are called complementary angles.
Supplementary angle: Two angles whose sum is 180° are called supplementary angles.
Adjacent angles: Two angles are adjacent if they have a common vertex, a common arm, and their non-common arms are on different sides of the common arm.
Linear pair: Two angles form a linear pair if their non-common arms form a line.
Vertically opposite angles: Vertically opposite angles are formed when two lines intersect each other at a point.
Transversal: A transversal crosses two or more lines at different points.
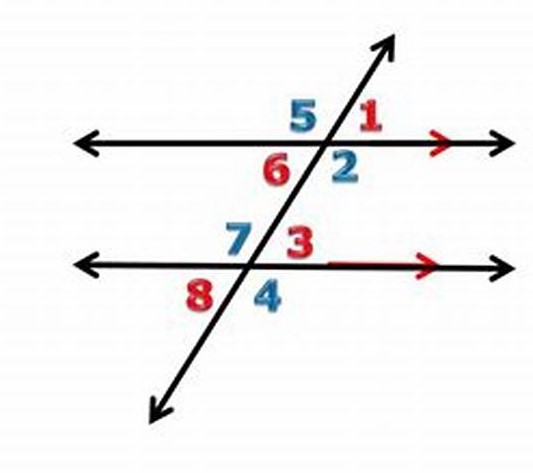
Alternate interior angles- Two angles that lie between two parallel lines on opposite sides of the transversal (but not a linear pair).
∠6=∠3 and ∠2=∠7
Alternate Exterior angles- Two angles that lie between outside the parallel lines on opposite sides of the transversal.
∠1=∠8 and ∠5=∠4
• A transversal intersects two parallel lines, then
(i) Each pair of corresponding angles is equal.
(ii) Each pair of alternate interior angles is equal.
(iii) Each pair of interior angle on the same side of the transversal is supplementary.
If a transversal interacts two lines such that, either
(i) Any one pair of corresponding angles is equal, or
(ii) Any one pair of alternate interior angles is equal or
(iii) Any one pair of interior angles on the same side of the transversal is supplementary then the lines are parallel.
• Lines which are parallel to a given line are parallel to each other.
•The sum of the three angles of a triangle is 180°
• If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.
🔍 Frequently Asked Questions (FAQs) on Lines and Angles
Question 1. What are complementary and supplementary angles?
Answer: Complementary angles add up to 90°, supplementary angles add up to 180°.
Question 2. How many types of angle pairs are there?
Answer: Five: Complementary, Supplementary, Adjacent, Linear Pair, and Vertically Opposite Angles.
Question 3. Are vertically opposite angles always equal?
Answer: Yes, always.
Question 4. What is the total sum of angles in a triangle?
Answer: 180°.




