Polynomials

Polynomials play an important role in creating the foundation for algebra. A polynomial is a mathematical expression that consists of variables, coefficients, and non-negative integer exponents combined using addition, subtraction, and multiplication.

What is a polynomial?

 An algebraic expression in which the variables involved have only non-negative integral powers is called a polynomial.
Example: 5x³+ 4x² +6x – 3 is a polynomial in variable x and Polynomials are denoted by p(x), q(x), r(x), etc.
If power of the variable (e.g., x, y) is negative integers, fractional numbers or irrational numbers, then the algebraic expression is not a polynomial.
Example: x^-2+x-9 or y^1/2+y+1

Important Terms in Polynomials:

Constant: A symbol having a fixed numerical value is called a constant.
Variable: A symbol which may be assigned different numerical values is known as variable.
Algebraic expression: A combination of constants and variables. Connected by some or all of the operations \(+, -,\times \) and is known as algebraic expression.
Terms: The several parts of an algebraic expression separated by ‘+’ or ‘-‘ operations are called the terms of the expression.

Coefficients: In the polynomial ax³bx²+cx+d, coefficient of x³, x², x are a, b, c respectively and also say that d is the constant term in it.

Degree of a polynomial in one variable: In case of a polynomial in one variable the highest power of the variable is called the degree of the polynomial.

Classification of polynomials on the basis of degree:

1. Linear polynomial: A polynomial having one degree is called a linear polynomial. e.g., ax+b , where a≠0.
2. Quadratic polynomial: A polynomial having two degree is called a Quadratic polynomial. e.g., ax²+bx+c, where a≠0.
3. Cubic polynomial: A polynomial having three degree is called cubic polynomial. e.g., ax³+bx²+cx+d, where a≠0.
4. Biquadratic polynomial: A polynomial having four degrees is called a biquadratic polynomial. e.g., ax⁴+bx³+cx²+dx+e, where a≠0.

Classification of polynomials on the basis of the number of terms:

1. Monomial polynomial:  A polynomial having only one term is called monomial polynomial. e.g. 7, 3x, 9x⁴, (1/2)y etc.
2. Binomial polynomial: A polynomial having two terms is called binomial polynomial. e.g.- 5x+6, x³+3². etc.
3. Trinomial polynomial: A polynomial having three terms is called trinomial polynomial. e.g.- 5x²-4x+9.. etc.
4. Constant polynomial: A polynomial having only one term, which is a constant term is called a constant polynomial and the degree of a non-zero constant polynomial is zero.
5. Zero polynomial: A polynomial having one term, namely zero only is called a zero polynomial and The degree of a zero polynomial is not defined.

Zeroes of a polynomial:

 Let p(x) be a polynomial. zeros of polynomial are the points where the polynomial becomes zero, i.e., If p(α) =0, then we say that α is a zero of the polynomial p(x).

Remainder theorem:

 Let f (x) be a polynomial of degree n ≥ 1 and let α be any real number. When f(x) is divided by (x – α) then the remainder is f (α).

Factor theorem:

 Let f(x) be a polynomial of degree n > 1 and let α be any real number then
(i) If f(α)=0 then (x-α )is the factor of polynomial f(x).

(ii) If (x-α) is a factor of polynomial f(x) then f(α)=0.

Factor:

 A polynomial p(x) is called factor of q(x) then p(x) divides q(x) Completely.

What is Factorization?

 To express a given polynomial as the product of polynomials each of a degree less than that of the given polynomial, such that no such factor has a factor of a lower degree, is called factorization.

Algebraic identities to help factorization:

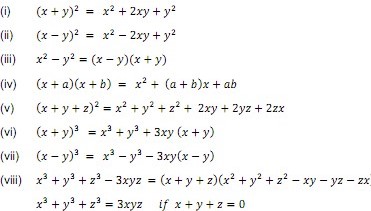
Some Important question on Polynomials

Question 1: Find the degree of the polynomial \(5x^{3]+3x^{2}-7x+9 \).

Answer: 3

Question 2: Factorize \(x^{2}-16 \).

Answer: \((x-4)(x+4)\)

🔍 Frequently Asked Questions (FAQs) on Polynomials

Q1: Can a polynomial have negative exponents?
A: No, the exponents must be non-negative integers.

Q2: What is the degree of a constant polynomial?
A: The degree of a non-zero constant polynomial is 0.

Q3: Is \(2^{-3} +5x-7 \) a polynomial?
A: No, because \(2^{-3} \) has a negative exponent.