In mathematics, we often deal with groups of objects or numbers. To handle these groups in a logical and structured way, we use the concept of sets. A set is a basic idea that helps us organize a collection of objects, and it can be represented in roster and set-builder form.
In set theory, you will learn about different types of collections, their properties, symbols, operations, and Venn diagrams.
What is a set?
A set is a collection of well-defined objects. These objects are called elements or members of the collection. The word “well-defined” means there is no confusion about whether an object belongs to the collection or not. It is denoted by a capital letter. Example: Let collection A={1,2,3,4,5}, where 1, 2, 3, 4, and 5 are the elements of collection A. It is described as \(1\in A\)
Examples of some important sets and their notations:
- N: The set of natural numbers.
- W: The set of whole numbers.
- I or Z: The set of integer numbers.
- R:The set of the real numbers.
- Q: The set of the rational numbers.
Representation of sets
Sets can be represented in two main ways:
- Roster form or tabular form: In this form, all elements are listed, separated by commas, inside curly brackets.
Example: A={1,3,5,7,9}. - Set-builder form: In this form, a rule or condition is given to define the elements.
Example: A={x|x is an odd number less than 10}.
Types of sets
- Empty set or null set or void set: A set which does not contain any elements is called an empty set. It is denoted by {} or \(\phi\).
Example: (i). The set of odd numbers divisible by 2. (ii). A={x: x\(\in \)N and 1<x<2}=\(\phi\). - Singleton set: A set which contain only single element is called singleton set.
Example: A={2} - Finite set: A set which is empty or consists of a definite number of elements is called a finite set.
Example: A= {1,2,3,4,5}. - Infinite set: A set which consists of an indefinite number of elements is called an infinite set.
Example: A={1,2,3,4,…) - Equal sets: Two sets A and B are said to be equal if they have exactly the same elements.
Example: If A={1,2,3} and B={2,3,1} then A=B - Equivalent set: If set A and set B are two different sets, if their number of elements is equal, they are called equivalent sets.
Example: If A={2,3,4,5} and B={a,b,c,d} ,where number of elements of A=n(A)=4 and number of elements of B=n(B)=4 \(\Rightarrow\) n(A)=n(B) - Subset: Set A is a subset of B if every element of A is in B. It is denoted by \(A\subseteq B\).
Example: A={1,2,3} and B={1,2,3,4} \(\Rightarrow\) \(A\subseteq B\)
Note: \(\phi\) is always a subset of any set. - Power set: The collection of all subsets of a set.
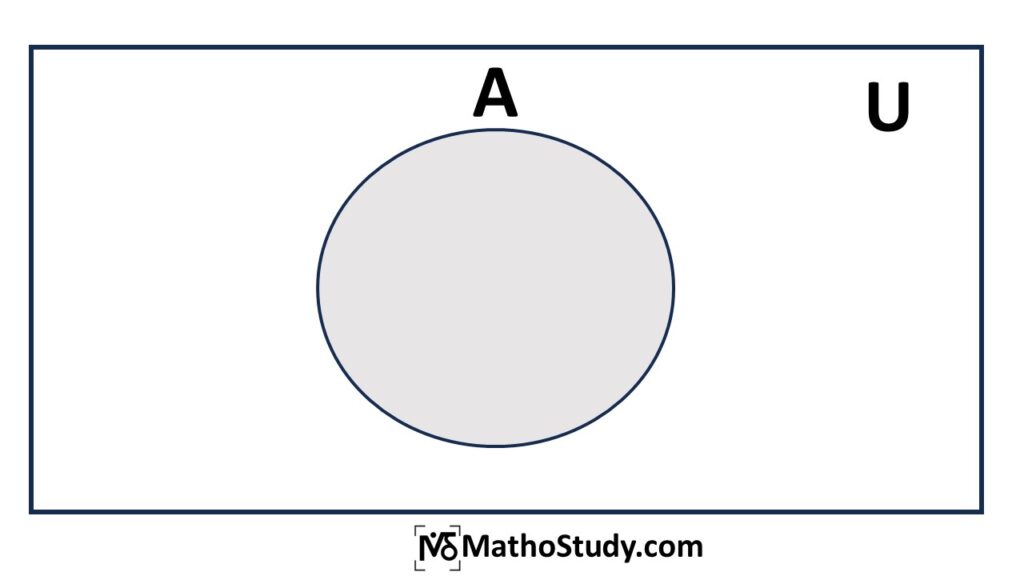
Example: If A={1,2}, then power set of A =P(A)={\(\phi\), {1}, {2}, {1,2}}. - Universal set: A set that contains all the elements under consideration. It is denoted by U.
Example: If A={1,3,4,5} and B={2,3,6,7}, then universal set will be U={1,2,3,4,5,6,7}
Operations on sets
- Union of sets: The union of two sets A and B is the set of all elements, which are either in A or B or both in A and B. It’s denoted by \(A\cup B \). i.e., \(A\cup B \) ={x:\(x \in A \) or \(x \in B \)}
Example: If A={1,2,3,4} and B={3,4,5,6}, then A union B is;
\(A\cup B \)={1,2,3,4,5,6} - Intersections of sets: The intersection of two sets A and B is the set of all elements, which are common to both A and B. Its denoted by \(A\cap B \). i.e., \(A\cap B \) ={x:\(x \in A \) and \(x \in B \)}.
Example: If A={1,2,3,4} and B={3,4,5,6}, then A intersection B is;
\(A\cap B \)={3,4} - Disjoint sets: If sets A and B are disjoint, then the set does not contain any common elements.Example: Set A={1,2,3} and set B={4,5} are disjoint becouse there is no common element. i.e., \(A\cap B=\phi \)
- Difference of sets: If set A and set B are two sets, then set A difference set B is a set which has elements of A but not of B. It is denoted by A-B. Example: If A={1,2,3,4} and B={3,4,5}, then A minus B is;
\(A- B \)={1,2} - Complements of sets: the complement of any set A is the set of all elements of the universal set which are not the elements of A. It is denoted by \(A’ \) or \( A^c \).Example: If A={1,2,3} and U={1,2,3,4,5}, then complement of A is;
\(A^c \)=U-A={4,5}
Properties of complements:
- \(A\cup A’ \)=U
- \(A\cap A’ \)=\(\phi \)
- (\(A\cup B \))’=\(A’\cap B’ \) or (\(A\cap B \))’=\(A’\cup B’ \)
- \((A’)’ \)= \(A\)
- \(U’\)=\(\phi\)
- \(\phi\)’=\(U\)
What is a Venn diagram?
A Venn diagram is a visual tool used to show relationships between sets. It uses overlapping circles to represent different sets.
- Each circle represents a set.
- Overlapping areas show elements common to the sets. i.e., intersection
- Non-overlapping areas show elements unique to each set.
- The rectangle enclosing all circles usually represents the universal set.
Properties of sets
i. Associative property:
- A\(\cup\)(B\(\cup\)C)=(A\(\cup\)B)\(\cup\)C
- A\(\cap\)(B\(\cap\)C)=(A\(\cap\)B)\(\cap\)C
ii. Commutative property:
- \(A\cup B\)=\(B\cup A\)
- \(A\cap B\)=\(B\cap A\)
iii. Distributive property:
- A\(\cup\)(B\(\cap\)C)=(A\(\cup\)B)\(\cap\)(A\(\cup\)B)
- A\(\cap\)(B\(\cup\)C)=(A\(\cap\)B)\(\cup\)(A\(\cap\)B)
iv. De Morgan’s law:
- (\(A\cup B \))’=\(A’\cap B’ \)
- (\(A\cap B \))’=\(A’\cup B’ \)
v. Complement law:
- \(A\cup A’ \)=U
- \(A\cap A’ \)=\(\phi \)
- \((A’)’ \)= \(A\)
- \(U’\)=\(\phi\)
- \(\phi\)’=\(U\)
Types of intervals
(i). Open interval: (a, b)={\(x\in R\): a<x<b} i.e., all the points between a and b belong to the open interval.
(ii).Closed interval: [a,b]={\(x\in R\): \(a\leq x \leq b\)} i.e., the interval which contains the end points also, is called closed interval.
(iii). Semi open or semi closed interval:
(a,b]={\(x\in R\): \(a<x \leq b\)}
[a,b)={\(x\in R\): \(a\leq x < b\)}
Some important formulas:
| Formula Expression | Description |
|---|---|
| \(n(A\cup B ) \)=\( n(A)+n(B)\)\(-n(A\cap B) \) | Determines the number of elements in the union of two sets A and B by adding their individual numbers and subtracting the numbers of their intersection. |
| \(n(A\cup B ) =\) \(n(A)+n(B) \) if \(A\cap B =\phi \) | If sets A and B are disjoint, then their union is simply the sum of their numbers. |
| \(n(A-B)+n(A\cap B)\) \(=n(A) \) | The number of set A can be calculated by adding the number of the difference of A and b to the number of their intersection. |
| \(n(B-A)+n(A\cap B)\) \(=n(B) \) | Similarly, the number of set B can be calculated by adding the number of the difference of B and A to the number of their intersection. |
| \(n(A\cup B \cup C)=\) \(n(A)+n(B)+n(C)\) \(-n(A\cap B)-n(B\cap C)-\)\(n(C\cap A)+n(A\cap B\cap C)\) | Determines the number of elements in the union of three sets A, B and C by considering all possible intersections to avoid over-counting elements present in multiple sets |
Some important questions:
Question 1: If \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \), find:
- \( A \cup B \)
- \( A \cap B \)
- \( A – B \)
- \( B – A \)
Solution:\[ \begin{aligned} \text{(1) } A \cup B &= \{1, 2, 3, 4, 5\} \\ \text{(2) } A \cap B &= \{3\} \\ \text{(3) } A – B &= \{1, 2\} \\ \text{(4) } B – A &= \{4, 5\} \end{aligned} \] Question 2: Let \( U = \{1,2,3,4,5,6,7,8,9,10\} \), \( A = \{2,4,6,8\} \), \( B = \{1,2,3,4\} \). Find:
- \( A’ \)
- \( B’ \)
- \( A \cup B \)
- \( A \cap B \)
Solution:\[ \begin{aligned} \text{(1) } A’ &= U – A = \{1,3,5,7,9,10\} \\ \text{(2) } B’ &= U – B = \{5,6,7,8,9,10\} \\ \text{(3) } A \cup B &= \{1,2,3,4,6,8\} \\ \text{(4) } A \cap B &= \{2,4\} \end{aligned} \]
Question 3: If the universal set \( U = \{1, 2, 3, 4, 5\} \), and \( A = \{2, 4\} \), find the complement of \( A \).
Solution:\( A’ = U – A = \{1, 3, 5\} \)
Question 4: If \( A = \{x : x \text{ is a letter in the word “APPLE”}\} \) and \( B = \{x : x \text{ is a letter in the word “PEAR”}\} \), find \( A \cup B \), \( A \cap B \), and \( A – B \).
Solution: \[ \begin{aligned} A &= \{A, P, L, E\} \\ B &= \{P, E, A, R\} \\ A \cup B &= \{A, P, L, E, R\} \\ A \cap B &= \{A, P, E\} \\ A – B &= \{L\} \end{aligned} \]
Question 5: If \( A = \{1, 2\} \), find the power set \( \mathcal{P}(A) \).
Solution: \( \mathcal{P}(A) = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} \)
Frequently asked questions on sets
Q1. What is set? Give an example.
Answer: A set is a well-defined collection of objects.
Example: {1, 2, 3, 4, 5} is a set of numbers
Q2. What are the different forms of sets?
Answer: There are two forms in which we represent the sets. They are:
(i). Roster form: A={1,3,5,7,9,11}
(ii). Set builder form: A={x:x=2n-1, \(n\in N \) and \(1\leq n\).
Q3. What is a Venn diagram?
Answer: A Venn diagram is a visual tool used to show relationships between sets. It uses overlapping circles to represent different sets.
Q4. What are the applications of sets?
Answer: Mathematics: For probability, relations, functions, etc.
Computer Science: To manage data and logic structures.
Database Management: To search and retrieve data efficiently.
Daily Life: Grouping people by age, interests, or profession.